量子几何张量是一个刻画量子系统几何性质的重要物理量,它的虚部对应着人们熟知的贝里曲率,在凝聚态物理、量子物理和光学等领域中都有着十分重要的应用;它的实部则对应着黎曼度规,用来定义两个相邻的量子态在参数空间中的“距离”,与量子精密测量理论中的量子费舍信息关系密切。近些年来,随着研究的深入,量子几何张量的重要性正在逐渐显现。例如:它与平带中的超流效应,轨道磁性,受激兰姆位移和非绝热反常霍尔效应等都相关。由于量子几何张量在拓扑物理、量子信息处理以及精密测量等领域的重要应用,因此,实现对量子几何张量的完整测量在实验上是十分必要的。
华中科技大学蔡建明以及张少良领导的研究团队与日本理化研究所Tomoki Ozawa、比利时布鲁塞尔自由大学的Nathan Goldman、德国乌尔姆大学的Martin B. Plenio、Fedor Jelezko合作,在《国家科学评论》(National Science Review)发表论文“Experimental measurement of the quantum geometric tensor using coupled qubits in diamond”,首次在固态自旋体系中实现了对量子几何张量这一重要物理量的直接完整测量。(博士研究生余民、博士研究生杨朋成为该论文共同第一作者)。

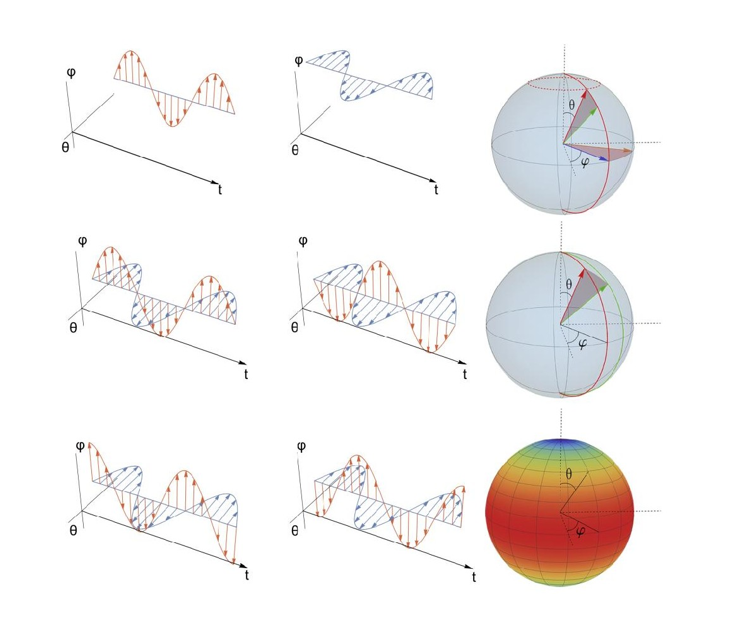
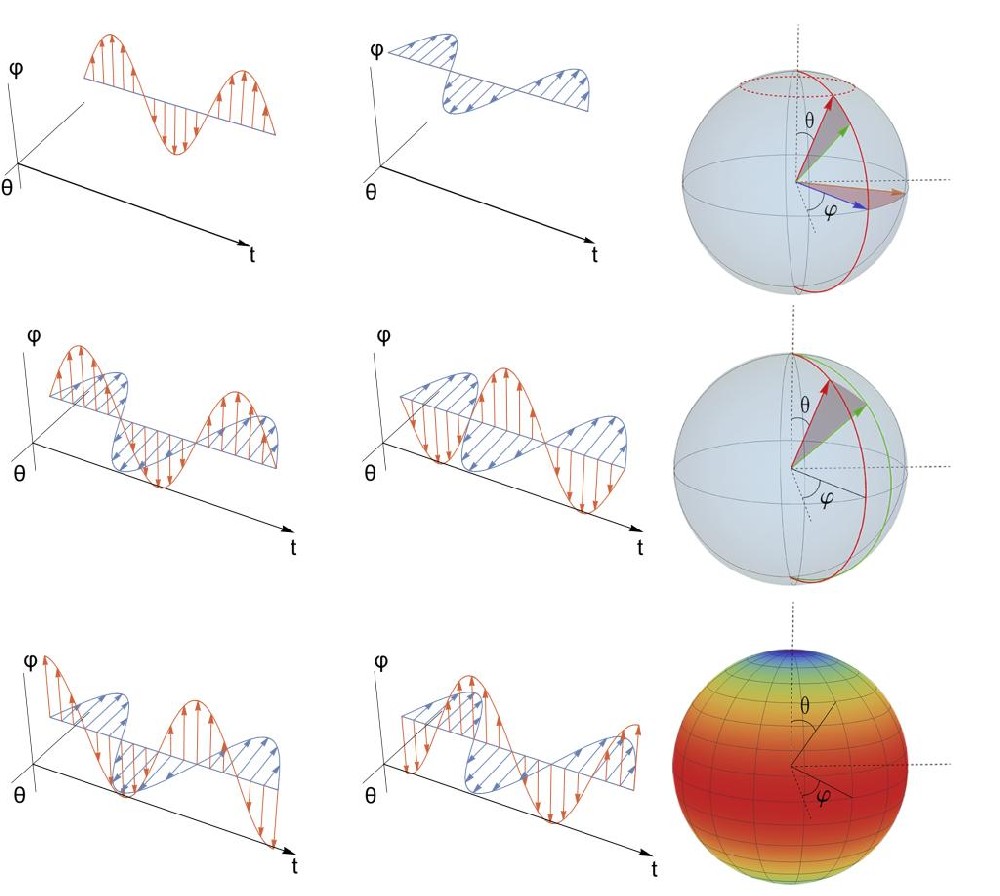
基于金刚石色心的二能级系统可以通过微波和激光脉冲精确控制,本实验首先利用特殊设计的微波场与金刚石氮-空位中心自旋的耦合在参数空间中模拟了一个“单极子”(monopole)结构。在此基础上,研究者们利用参数调制技术(图(a)和图(b)对应线性参数调制,图(c)对应椭圆参数调制),通过对相应参数外加周期性调制,利用一个动力学过程来实现对相应量子几何张量矩阵元的测量,即利用参数调制诱导的拉比跃迁的频率和量子几何张量决定的跃迁矩阵元之间的联系来测量量子几何张量。研究者第一次在固态自旋体系实验上证实此种技术能够直接测量黎曼度规,并可同样精确地测量量子几何张量的其他张量矩阵元。此外,研究者们还将此方法扩展到一个金刚石色心和碳13核自旋耦合所组成的双比特系统,并成功在这个自旋耦合体系中实现了对量子多体系统完整量子几何张量的直接测量。这些结果证实量子相干动态响应可以作为一种测量量子系统几何和拓扑性质的强大工具,并为探索量子几何张量在物理学各个领域中的应用开辟了新道路。
相关论文:Experimentalmeasurement of the quantum geometric tensor using coupled qubits in diamond,Min Yu, Pengcheng Yang, Musang Gong, Qingyun Cao, Qiuyu Lu, Haibin Liu, Shaoliang Zhang, Martin B Plenio, Fedor Jelezko, Tomoki Ozawa, Nathan Goldman, Jianming Cai, NationalScience Review, nwz193 (2019) .